

We can still use geodesic deviation if we start out with a family of geodesic curves that are not perpendicular to some baseline. In that simplest case, we started out with a family of geodesic curves perpendicular to some base line and checked whether they converged or diverged. So far, we have just considered the simplest case of geodesic deviation. There are three cases corresponding to the three geometries. That tells us immediately what sort of space we are in. We then proceed along the perpendiculars, noticing whether they converge or diverge (or neither). We start with a straight (geodesic) line and erect straight (geodesic) perpendiculars on it. If we are in a curved space, here is a convenient way to determine the curvature without having to resort to a higher dimensioned embedding space. We will develop these means below, first for the familiar case of spaces of constant curvature. Locally, that is, it works in tiny little patches of the space. But if the curvature of the space varies a great deal over the region of space covered by the triangle, that sum will not tell us much of any use. We could draw very big triangles to check how the sums of their angles differ from 180 o. The curvature at each place? Since the curvature varies from place to place, the methods that we learned in the last chapter will be of limited use. If we have a space of variable curvature, how do we determine It is just a dimpled surface shown here, with flat parts, dome-like parts with positive curvature and saddle-like parts with negative curvature. A surface with that sort of geometry is not hard to visualize. We can investigate surfaces that have curvatures that vary from place to place: no curvature here positive curvature there even more positive curvature somewhere else and negative curvature in yet another place.
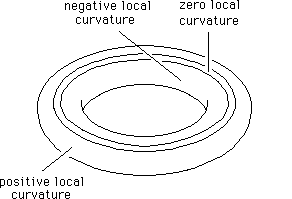
Nothing makes us to restrict ourselves to surfaces like the surface of a sphere.
Positively and negatively curved space Patch#
This means that the geometry of each little patch of the sphere's surface is same as every other little patch.
Its intrinsic geometry has positive curvature and that curvature is the same everywhere. A simple example is just the surface of a sphere. Or if it has positive curvature in one place, we have assumed it has the same positive curvature everywhere else. This means that if a space is flat in one place, we have assumed it is flat everywhere. That is, we have been examining spaces that are everywhere the same, geometrically. So far, we have examined the geometry of homogeneous A Space with Different Curvature in Different DirectionsĮuclid's Postulates and Some Non-Euclidean Alternatives.Curvature in Different Directions of a Higher Dimensioned Space.Geodesic Deviation in Spaces of Variable Curvature.


 0 kommentar(er)
0 kommentar(er)
